Haskell is often considered a paradigmatic functional programming language for several reasons:

1. Purity and Immutability:

   • Haskell is a purely functional language, which means that functions in Haskell are referentially transparent and side-effect-free. This purity ensures that the result of a function depends only on its inputs, promoting clarity and reasoning about code.

   • Immutability is enforced by default in Haskell. Once a value is bound to a name, it cannot be changed. This immutability simplifies reasoning about program state and helps avoid bugs related to mutable data.

2. Lazy Evaluation:

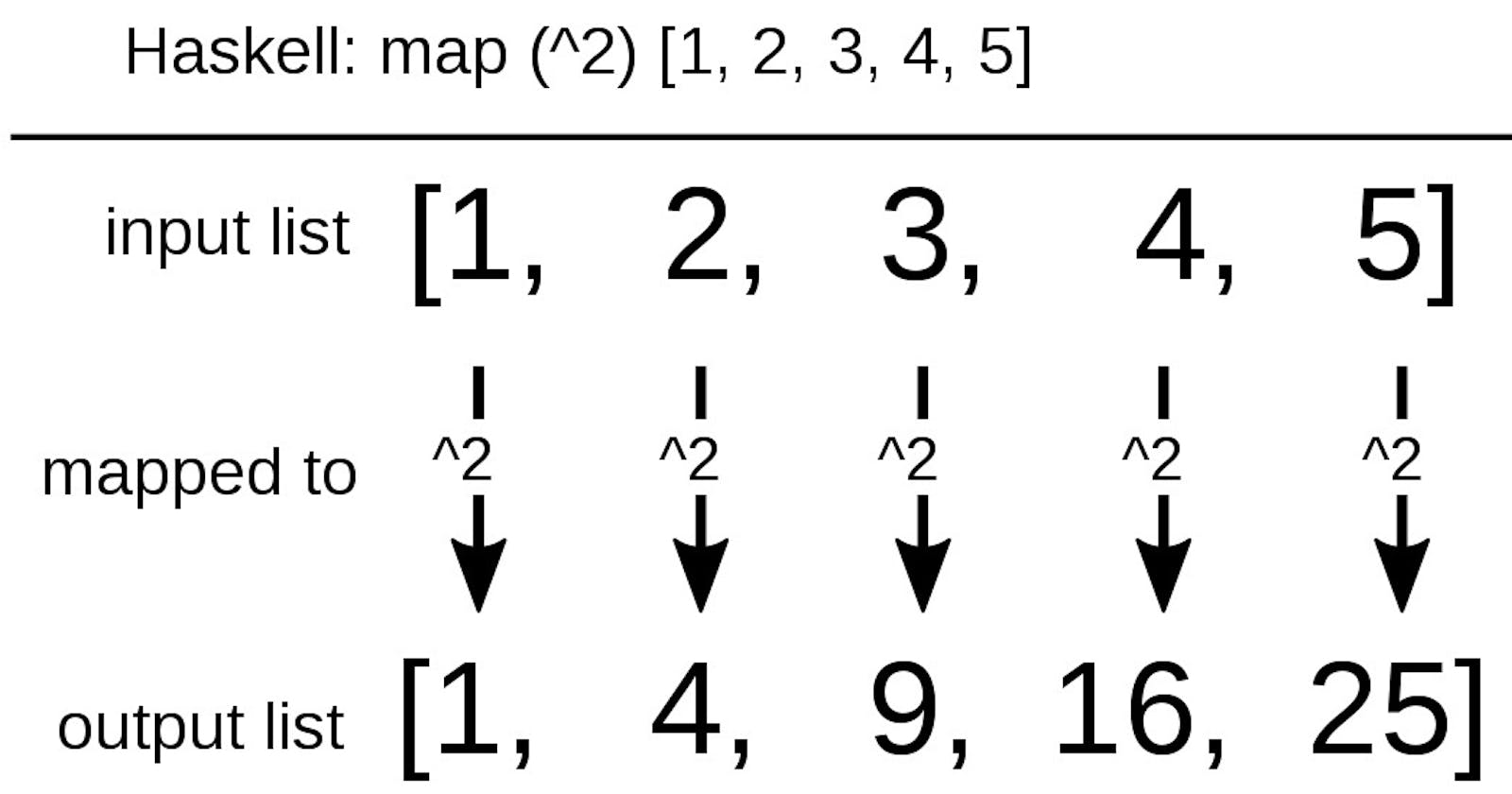
   • Haskell employs lazy evaluation, where expressions are not evaluated until their values are actually needed. This enables the creation of infinite data structures and allows for more modular and composable code.

   • Lazy evaluation helps avoid unnecessary computations, leading to potentially more efficient and expressive programs.

3. Type System and Type Inference:

   • Haskell has a strong, static type system that is based on Hindley-Milner type inference. The type system helps catch errors at compile time, providing a high level of safety.

   • Haskell's type system also supports polymorphism, type classes, and algebraic data types, allowing for expressive and concise code.

4. Higher-Order Functions and First-Class Functions:

   • Haskell treats functions as first-class citizens, meaning functions can be passed as arguments to other functions, returned as values, and stored in data structures. This enables the use of higher-order functions, facilitating functional programming patterns.

   • Higher-order functions in Haskell promote code that is concise, modular, and expressive.

5. Pattern Matching and Algebraic Data Types:

   • Pattern matching in Haskell allows for concise and readable code when working with algebraic data types. This feature makes it easy to destructure and process complex data structures.

   • Algebraic data types, including sum types (enums) and product types (structs), provide a powerful mechanism for modeling data in a clear and extensible way.

6. Monads and Monadic I/O:

   • Haskell introduced the concept of monads to handle side effects in a pure functional setting. Monads allow sequencing of computations while maintaining referential transparency.

   • The use of monads in Haskell enables a clean and principled approach to handling input/output operations in a functional language.

7. Expressive Type Classes:

   • Haskell's type classes allow ad-hoc polymorphism, enabling the definition of common operations for various types. This leads to more generic and reusable code.

   • The use of type classes in Haskell is a powerful mechanism for creating abstract interfaces and promoting code that is both expressive and modular.

The combination of these features makes Haskell a paradigmatic functional programming language. It serves as a reference for functional programming principles and has influenced the development of other functional languages. Haskell's design choices encourage developers to adopt a functional programming mindset, leading to code that is often concise, elegant, and maintainable.

Here's an example that demonstrates the principles of recursion, higher-order functions, immutability, and referential transparency:

-- Example of recursion
factorial :: Integer -> Integer
factorial 0 = 1
factorial n = n * factorial (n - 1)

-- Example of a higher-order function (map)
multiplyByTwo :: [Integer] -> [Integer]
multiplyByTwo = map (*2)

-- Example of immutability
originalList :: [Integer]
originalList = [1, 2, 3, 4, 5]

-- Applying a higher-order function to the original list
doubledList :: [Integer]
doubledList = multiplyByTwo originalList

-- Referentially transparent function
addTwo :: Integer -> Integer
addTwo x = x + 2

main :: IO ()
main = do
  -- Example of immutability
  let originalValue = 5
  putStrLn $ "Original value: " ++ show originalValue

  -- Referentially transparent function
  let doubledValue = addTwo originalValue
  putStrLn $ "Doubled value: " ++ show doubledValue

  -- Example of recursion
  let result = factorial 5
  putStrLn $ "Factorial of 5: " ++ show result

  -- Example of a higher-order function (map)
  putStrLn "Original list: " ++ show originalList
  putStrLn $ "Doubled list: " ++ show doubledList

In this Haskell example:

• Recursion: The factorial function calculates the factorial of a number using recursion.

• Higher-order function (map): The multiplyByTwo function is defined using the map higher-order function, which multiplies each element of a list by 2.

• Immutability: In Haskell, variables are immutable. The originalList and doubledList values are bound to names, and once assigned, their values do not change.

• Referential Transparency: The addTwo function is referentially transparent. Given the same input, it will always produce the same output.

Note: Haskell uses a lazy evaluation strategy, which means that values are only computed when needed. This can have a profound impact on how functions are evaluated and how recursion is handled.

In C, achieving full functional programming principles such as immutability and referential transparency can be challenging due to the mutable nature of variables. However, you can still demonstrate functional programming concepts like recursion and higher-order functions. Here's a simple example that showcases recursion and a basic form of a higher-order function in C:

#include <stdio.h>

// Example of a higher-order function
typedef int (*UnaryOperation)(int);

// Higher-order function that applies a unary operation function to each element of an array
void map(int* array, size_t size, UnaryOperation op) {
    for (size_t i = 0; i < size; ++i) {
        array[i] = op(array[i]);
    }
}

// Example of a recursive function
int factorial(int n) {
    if (n == 0 || n == 1) {
        return 1;
    } else {
        return n * factorial(n - 1);
    }
}

int main() {
    // Example of immutability (const) --------------------------------
    const int originalValue = 5;
    printf("Original value: %d\n", originalValue);

    // Example of referential transparency (pure function) ------------
    int doubledValue = originalValue * 2;
    printf("Doubled value: %d\n", doubledValue);

    // Example of recursion -------------------------------------------
    int result = factorial(5);
    printf("Factorial of 5: %d\n", result);

    // Example of a higher-order function (map) -----------------------
    int numbers[] = {1, 2, 3, 4, 5};
    size_t arraySize = sizeof(numbers) / sizeof(numbers[0]);

    // Define a unary operation function (double)
    int doubleOperation(int x) {
        return x * 2;
    }

    // Apply the double operation using the map function
    map(numbers, arraySize, doubleOperation);

    // Print the modified array
    printf("Doubled array: ");
    for (size_t i = 0; i < arraySize; ++i) {
        printf("%d ", numbers[i]);
    }
    printf("\n");

    return 0;
}

In this example:

• Immutability: The const keyword is used to declare a constant (originalValue), demonstrating a form of immutability. However, note that C does not enforce immutability in the same way as functional languages.

• Referential Transparency: The expression originalValue * 2 is referentially transparent, meaning it will always produce the same result for the same inputs.

• Recursion: The factorial function is a recursive function that calculates the factorial of a number.

• Higher-order function (map): The map function takes an array, its size, and a unary operation function (op). It applies the unary operation to each element of the array, demonstrating a basic form of a higher-order function.

While this example incorporates some functional programming principles, it's important to note that C is not a purely functional language, and achieving true immutability and referential transparency might require a different programming paradigm.